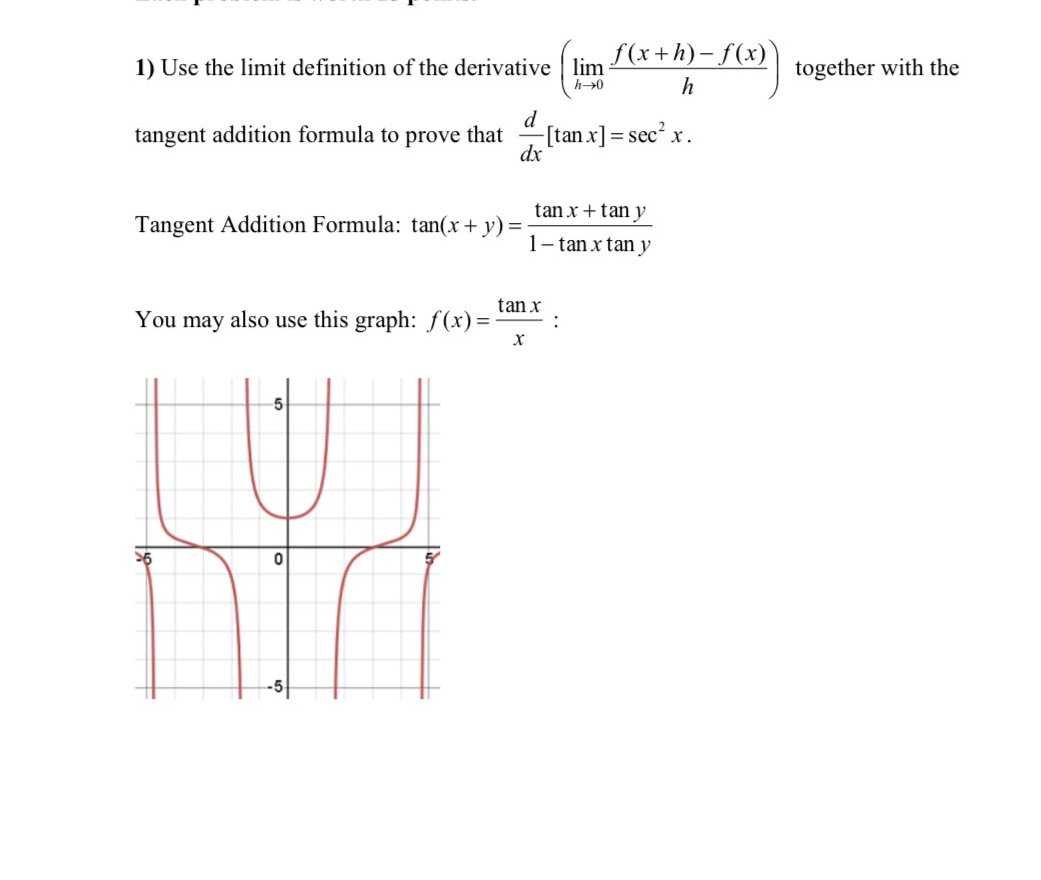
Prelimilaries: \(\lim _ { h \to 0} \frac { \tan h} { h} = 0\); \(\lim _ { h \to 0} 1 - \tan x \tan h = 1\).
By using the prelimilaries, we have:
\(( \tan x) ' = \lim _ { h \to 0} \frac { \tan ( x+ h) - \tan ( x) } { h} = \lim _ { h \to 0} \frac { \frac { \tan ( x) + \tan ( h) } { 1 - \tan ( x) \tan ( h) } - \tan ( x) } { h} = \lim _ { h \to 0} \frac { \tan ( x) + \tan ( h) - \tan ( x) + \tan ^ 2( x) \tan ( h) } { h( 1- \tan ( x) \tan ( h) ) } = \lim _ { h \to 0} \frac { 1 + \tan ^ 2( x) } { 1 - \tan ( x) \tan ( h) } \cdot \frac { \tan ( h) } { h} = 1 + \tan ^ 2( x) = \sec ^ 2x\)